A. Computer Game
Solution:
Scan from left to right one by one. As long as one of the columns on the left can be reached, all safe cells in the current column can be reached.
Code:
Java

C++

B. Groups
Solution:
Enumerate which two days are in lesson. As long as everyone can have lesson in these two days, and more than half of the people can come to lesson in each lesson , a way of dividing will definitely be found.
Consider the worst-case scenario, the half who can come on a certain day can only come on that day. According to the above conditions, the remaining half must can come on another day.
Code:
Java

C++

C. Delete Two Elements
Solution:
Let the sum of all the elements of the original array be sum, and the two deleted numbers are x and y respectively. According to the question, there must be $\frac {sum} n = \frac {sum - x -y} {n-2}$. So naturally there is $sum \cdot (n-2) = (sum-x -y) \cdot n$.
Obviously the value of x+y is a fixed value. Therefore, as x increases, y must decrease. So we sort the original array and enumerate x in turn.
The only thing to note during the enumeration process is that the original array may have the same elements, so we need to count the number of times each number appears, and de-duplicate the original array.
Code:
Java

C++

D. Training Session
Solution:
Consider the case that both of the two conditions are not met. It is not difficult to notice that if you want neither of these conditions to be met, the difficulty or topic of the three questions cannot be the same.
Take the three questions with the same topic as a negative example. According to the definition of the problem, the difficulty of the three questions must be different at this time. Therefore, one of the conditions must be met.
Therefore, both difficult and topic have and only have two problems are the same. for example:
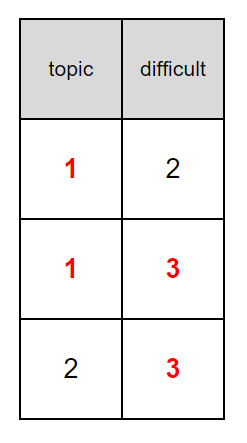
Obviously, according to the above picture, one of the three problems must be red for both difficult and topic at the same time. In the other two problems, one and only one's topic is red, and the other problem's difficult is red.
So we can enumerate the problem that topic and difficult are all red at the same time.
Code:
Java

C++

E. Staircases
Solution:
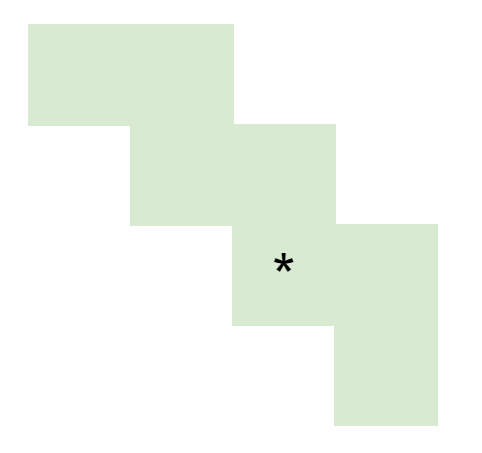
First of all, we found that each cell can be mapped into two staircase. Take the * cell in the following figure as an example, it can be mapped to the following two staircase:
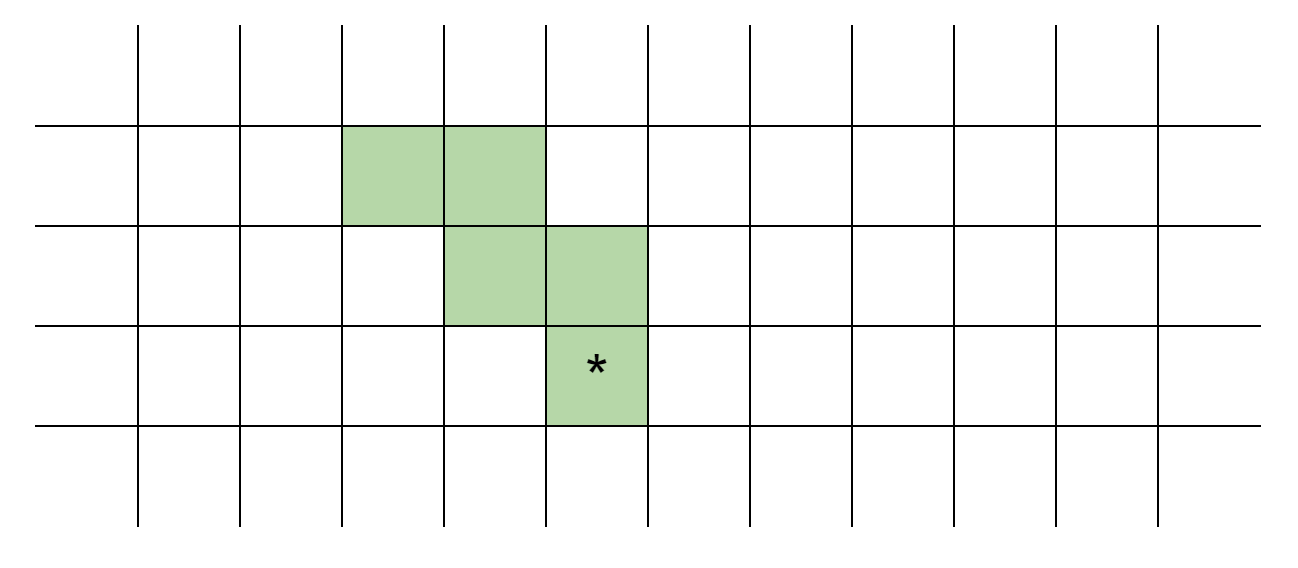
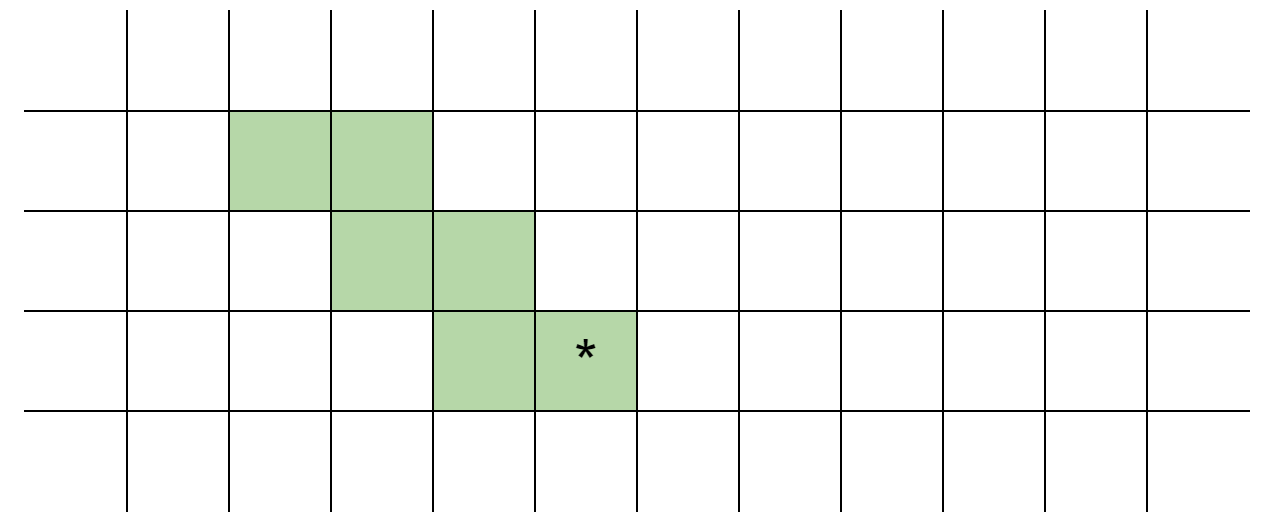
Similarly, the points below the diagonal can also be mapped to the two staircase:
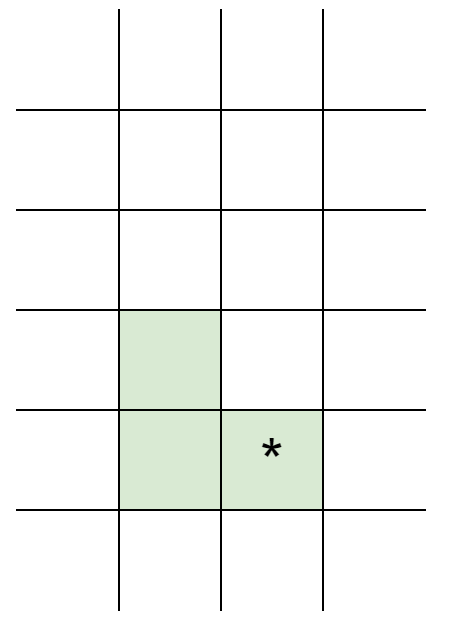
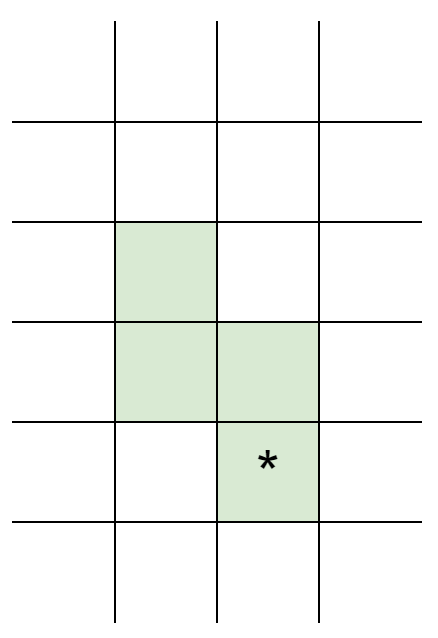
So it's obvious. When we change a cell, the effect of this cell will only affect the cells that between first locked cell on the up and down (that is, only related to the longest continuous staircase). Take the following picture as an example:
If we want to lock , the effect will be 53=15 different staircase, that is, any cells before * to any cell after * (including the cell of *).
The same goes for unlocking the locked cell.
Code:
Java

C++

I’m too busy with work lately, and I really don’t have time to read the F question.
