A. Arena
Solution:
If a hero is not the lowest level, then he can fight with lower-level heroes.
Code:
C++:

Java:

B. Cat Cycle
Solution:
To take the remainder easier. We change the napping spots index from 1-n to 0-(n-1). Also change the change the problem from "at hour k" to "after k hours". It still same thing.
Now we need calculate total steps which cat B moved. Not hard to find that: only if n is odd number, then every $\frac{n-1}{2}$ steps cat B will have one more step.
So, we can take the remainder and plus one as the answer.
Code:
C++

Java

C. Minimum Ties
Solution:
Can easily got this way: let $i$th team win the $i+1$th team.
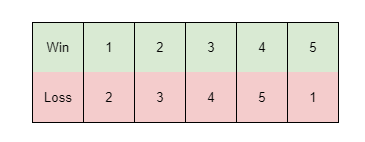
So we can extend this way: every time let $i$th team win the $i+diff$th team. If can make sure every time can win a round, then we can keep the score same.
And it not hard to find that: if the number of remain games is more than n, it must can let every team win one game.
Code:
C++

Java

D. Pythagorean Triples
Solution:
Because $a^2=c+b$, so, $2\leq a^2 \leq 2\cdot 10^9$. And so, we can enumerate the value of a.
Put $c=a^2-b$ in $a^2+b^2=c^2$, we can get $b=\frac{a^2-1}{2}$. And then we can get the value of $c$.
So, we can get all possible $c$ between 1 to $10^9$ in preprocess. And for each n, we binary search out the max possible c and the index of it. The answer should be the index + 1.
Code:
C++

Java

E. Cheap Dinner
Solution:
Let go with a brute force DP first. $dp[i][j]$ represent the minimum cost of i-th course choose type-$j$. (drink is course 3)
So $dp[i][j]=\min\limits_{1\leq x \leq n_i}{(dp[i-1][x])}+cost[i][j]$.
But it will get TLE if we get the $\min\limits_{1\leq x \leq n_i}{(dp[i-1][x])}$ by loop. So, we need some way to find this min value.
For the disallow list, we sort the list by $y$ first.
Then, we sort by the cost of $x$-type in $(i-1)$-th course. And at the same time, we sort dp[i-1] in the same way.
Then we can get the first allowed course with minimum cost. (Because the dp[i-1] also sorted)
Code:
C++

Java

