A. Gift Carpet
Solution:
Simply match column by column.
Code:
Java

C++

B. Sequence Game
Solution:
If $b_i \geq b_{i-1}$, there is no need to make any changes; just set $a_i = b_i$ and $a_{i-1} = b_{i-1}$.
For $b_i < b_{i-1}$, insert $b_i$ in the middle, i.e., $a_i = b_i$, $a_{i-0.5} = b_i$, and $a_{i-1} = b_{i-1}$.
Code:
Java

C++

C. Flower City Fence
Solution:
Calculate the length needed for placing the laid horizontally. For example, if you have [4, 2, 1] and you want to place them horizontally, it would be [3, 2, 1, 1], denoted as array b.
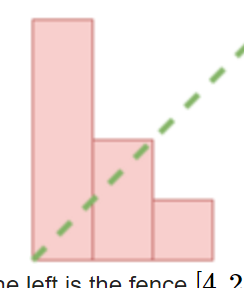
You can observe that for any x, if there are c indices i such that $a_i \geq x$, then the corresponding $b_x$ is equal to c.
For example, in [4, 2, 1], there are 3 elements greater than or equal to 1, so $b_1 = 3$. Thus, b = [3, 2, 1].
(In comparison to the actual horizontal placement, the last '1' was actually omitted, but it's not significant. This is because for $a_1$ to match n, it must be equal to n.)
Finally, compare the original array a with b. If they are the same, it's a YES; otherwise, it's a NO.
Code:
Java

C++

D. Ice Cream Balls
Solution:
Clearly, if there is only one of each ice cream ball type, you can make $C_x^2$ different ice creams for x types.
Since the problem allows combining two same ice cream balls into one, each type of ice cream ball can have at most two. Moreover, for every type that has two ice cream balls, you can create one more type of ice cream.
So, x types of ice cream balls (any quantity) can result in a minimum of $C_x^2$ different ice creams and a maximum of $C_x^2+x$ different ice creams.
You can perform binary search to find the minimum and maximum x needed to achieve the desired number of different ice creams.
Then, you can brute force each x within this range to find the minimum number of ice cream balls required.
Code:
Java

C++

E. Kolya and Movie Theatre
Solution:
Firstly, as long as you are not completely avoiding watching movies, the total mood points deducted for watching all movies, regardless of $a_i$, will only depend on the day of the last movie you watch.
For example, if you watch the last movie on the third day, you only need to subtract $3 \cdot d$. After that, it's irrelevant to d.
What's left to consider is the sum of several $a_i$ values. Naturally, you'd want to choose a positive $a_i$ as large as possible.
So, you can enumerate the day x when you watch the last movie. Then, you can use a priority queue to sort all $a_i$ values that were before the day x . If the length of the priority queue exceeds m, you discard the smallest values.
One issue is that $a_x$ might not be chosen as the last movie day. It's possible that the last movie day is actually y. However, since you deducted an extra $(x-y) \cdot d$, this will not lead to a better result than before.
Code:
Java

C++

F. Magic Will Save the World
Solution:
The time limit is 4 seconds, and Codeforces can handle more than $10^6$ operations per second. So, this $O(n \cdot \sum{s}) = O(n^2 \cdot s)$ solution with approximately $10^8$ operations can pass comfortably and runs in about 800ms (even in Java).
First, you can solve a 0/1 knapsack problem to find all possible total sums of these n monsters.
Once you have this total, you can binary search for the required time $ans$. Assuming it takes $ans$ seconds, you can then binary search for the largest combination that is less than $ans \cdot w$. If the remaining monsters can be defeated in less than $ans \cdot f$ time, you can defeat all monsters in $ans$ seconds.
Code:
Java

C++

G. The Great Equalizer
Solution:
Firstly, Java users should be cautious when using Java features, as it can lead to TLE (Time Limit Exceeded). For example, consider the following:

It's easy to observe that, no matter what, the difference between adjacent numbers in the sorted array will reduce by 1 each time.
Also, regardless of the transformation, smaller numbers will never exceed larger numbers; at most, they will become the same and merge.
So, if two adjacent close numbers need to become the same, and their difference is x, it will always take x steps.
Assuming b is the sorted version of a (just for explanatory purposes, not necessary to compute), the problem boils down to finding the maximum $b_i - b_{i-1}$ and the maximum $a_i$.
Maintaining the maximum $a_i$ is straightforward with a set.
In each operation, remove the old $a_i$ and add the new $a_i$ to the set.
You can also maintain the maximum $b_i - b_{i-1}$ using a set.
In each operation, find the two adjacent numbers of $a_i$ (denoted as pre_left and pre_right) and remove $a_i - \text{pre_left}$ and $\text{pre_right} - a_i$ from the set. Then, add $\text{pre_right} - \text{pre_left}$ to the set. So we effectively removing the old $a_i$.
Next, in the set that maintains the size of $a_i$, find the two adjacent numbers of the new $a_i$ (denoted as next_left and next_right) and remove $\text{next_right} - \text{next_left}$. Adding $a_i - \text{next_left}$ and $\text{next_right} - a_i$ to the set. So we effectively adding the new $a_i$.
Note that since the values of $a_i$ can be repeated, and hence $b_i - b_{i-1}$ can also be repeated, both sets should maintain both the value and the index.
Code:
Java

C++



