A. Polycarp and Sums of Subsequences
Solution:
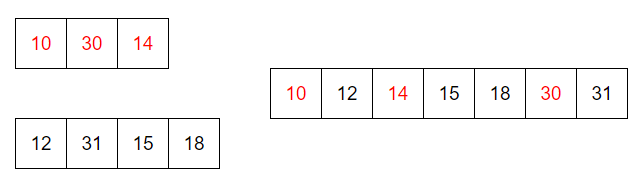
We assume a[1]<a[2]<a[3]. So naturally b[7]=a[1]+a[2]+a[3], b[6]=a[2]+a[3], b[5]=a[1]+a[3].
So a[1]=b[7]-b[6], a[3]=b[5]-a[1]. Finally a[2]=b[7]-a[1]-a[3].
Code:
Java

C++

B. Missing Bigram
Solution:
If the first character of the current string is equal to the last character of the previous string, then continue. If unequal is found, then a string must be missed here, just add it.
If the whole process is always equal, just add a character at the end.
Code:
Java

C++

C. Paint the Array
Solution:
Obviously this d is either the greatest common divisor of all odd digits or the greatest common divisor of all even digits. And this d must not divide any remaining number.
Code:
Java

C++

D. Array and Operations
Solution:
Obviously, we can perform the operation with as large a number as possible, and make the result of each operation to be 0 as much as possible.
Code:
Java

C++

E. Singers' Tour
Solution:
This is a problem of solving a linear equation (take n=5 as an example):$$\begin{cases}
1\cdot a_1 + 5\cdot a_2 + 4\cdot a_3 + 3\cdot a_4 + 2\cdot a_5=b_1 \\
2\cdot a_1 + 1\cdot a_2 + 5\cdot a_3 + 4\cdot a_4 + 3\cdot a_5=b_2 \\
3\cdot a_1 + 2\cdot a_2 + 1\cdot a_3 + 5\cdot a_4 + 4\cdot a_5=b_3 \\
4\cdot a_1 + 3\cdot a_2 + 2\cdot a_3 + 1\cdot a_4 + 5\cdot a_5=b_4 \\
5\cdot a_1 + 4\cdot a_2 + 3\cdot a_3 + 2\cdot a_4 + 1\cdot a_5=b_5 \\
\end{cases}$$
So, $15\cdot a_1 + 15\cdot a_2 + 15\cdot a_3 + 15\cdot a_4 + 15\cdot a_5=b_1+b_2+b_3+b_4+b_5$. And so, $a_1+a_2+a_3+a_4+a_5=\frac {b_1+b_2+b_3+b_4+b_5} {15}$。
We let $sum=\frac {b_1+b_2+b_3+b_4+b_5} {15}$
So that $$\begin{cases}
4\cdot a_2 + 3\cdot a_3 + 2\cdot a_4 + 1\cdot a_5=b_1-1\cdot sum \\
-1\cdot a_2 + 3\cdot a_3 + 2\cdot a_4 + 1\cdot a_5=b_2-2\cdot sum \\
-1\cdot a_2 + -2\cdot a_3 + 2\cdot a_4 + 1\cdot a_5=b_3-3\cdot sum \\
-1\cdot a_2 + -2\cdot a_3 + -3\cdot a_4 + 1\cdot a_5=b_4-4\cdot sum \\
-1\cdot a_2 + -2\cdot a_3 + -3\cdot a_4 + -4\cdot a_5=b_5-5\cdot sum \\
\end{cases}$$
We found that in the above formula, two adjacent expressions can find a value of a (not including $a_1$).
Finally, we can calculate $a_1$ based on other $a_i$.
During this process, we need to verify several points: 1. sum should be an integer; 2. $a_i$ cannot exceed the range; 3. $a_1$ must be calculated twice to ensure that there is a solution.
Regardless of the value of sum or the value of a, the solution process is $O(n)$.
Code:
Java

C++

F. Reverse
Solution:
Direct brute force search is enough. Because it is not difficult to find that adding 0 to the right is actually very difficult. In fact, adding 0 is difficult. Because 0 is added to the right and reversed, 0 will disappear. So the value that may appear is actually very limited, so direct brute force search is enough.
Code:
It is recommended to refer to the Java code. C++ has some optimizations due to the stack issue in the DFS process, which reduces the readability.
Java

C++

G. Trader Problem
This is a very good problem of Disjoint-set and offline processing.