Solution:
This problem is a typical application of segment tree.
As shown in the figure below, we maintain three attributes for each interval:
1. The number of subarray that meet the condition (mark as ans);
2. Starting from the leftmost side, the length of the longest continuous non-decreasing subarray (mark as left_size);
3. Starting from the rightmost, the length of the longest non-decreasing subarray (mark as right_size).
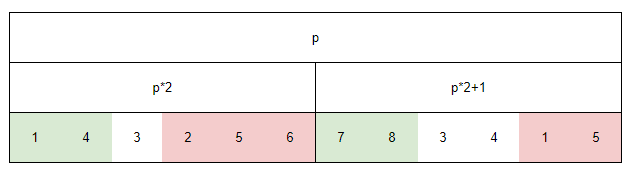
Take the above picture as an example, left size=2; right_size=3 in the p2 interval. The left_size=2; right_size=2 in the p2+1 interval.
It is not difficult to find that the right side of the p2 interval and the left side of p2+1 can be combined to a subarray. Therefore $$nodes[p].ans=nodes[p*2].ans+nodes[p*2+1].ans+\\nodes[p*2].right\_size*nodes[p*2+1].left\_size$$That is to say, without considering the combination of the right side of the p2 interval and the left side of p2+1, the ans of p is the sum of the ans of the left and right children.
But if it can be combined, then you need to add $$nodes[p*2].right\_size*nodes[p*2+1].left\_size$$
Code:
Java

C++

