A. Dislike of Threes
Solution:
Just check each number in turn starting from 1.
Code:
Java

C++

B. Who's Opposite?
Solution:
The total number of people is equal to $2\cdot |a-b|$, that is, the difference between a and b is half the number of people. If any number in a, b, c is greater than the total number of people, output -1. Otherwise, add or subtract $|a-b|$ according to the situation of c.
Code:
Java

C++

C. Infinity Table
Solution:
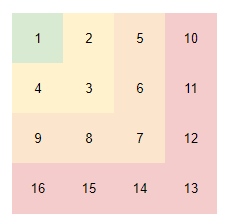
We segment as shown in the figure below. It is not difficult to find that the starting value of each segment is only increased by 2 each time.
Code:
Java

C++

D. Make a Power of Two
Solution:
Enumerate from $2^0$ to $2^63$. For each $2^k$, we match from high to low, and calculate the number of actions required. Finally, we choose the smallest one from the 64 answers.
Code:
Java

C++

E. Polycarp and String Transformation
Solution:
Because every time we delete a letter from s. Therefore, we go through t from back to front, according to the order of the first appearance of the letters, we can get the order of deleting the letters.
After we get the order of deletion, we can construct s from the total number of occurrences of each letter.
Finally, according to the s we constructed, just verify it.
Take the sample as an example:
As shown in the figure below, we check the first appearance order of each letter from right to left, so we get the deletion order: lcoayrp.

Then we try to build s. Obviously, because ‘l’ was the first to be deleted, all letters ‘l’ should be in s. Then for the letter ‘c’, because it is the second one to be deleted, the letter ‘c’ in s will appear twice in t. For the letter ‘p’, the number of letters ‘p’ in s is the number of letters ‘p’ in t divided by 7. So we can get the number of occurrences of each letter in s.
Finally, according to the number of occurrences of each letter in s, combined with t, we can get s. Verify again.
Code:
Java

C++

F. Nearest Beautiful Number (Easy/Hard)
Solution:
First, $C_{10}^5=252$. Therefore, we choose to enumerate these k numbers directly. Then construct a number that is as small as possible and greater than n according to the selected number.
As for the construction process, we need to pay attention to the following points.
1. If one of the previous digits is already greater than the original number, then all subsequent digits are chosen as small as possible.
2. If the original digit is larger than these k numbers, then go forward to find the nearest one, and increase the number of this one.
3. If there is no such position of point 2, then this arrangement is not valid.
Cod:
Java

C++



