A. Cherry
Solution:
Obviously, we want the max value and min value as large as possible. So that the product can be as large as possible. At least one of $$max(a_{l},a_{l+1})\cdot min(a_{l},a_{l+1}) \geq max(a_{l},a_{l+1},a_{l+2})\cdot min(a_{l},a_{l+1},a_{l+2})$$and$$max(a_{l+1},a_{l+2})\cdot min(a_{l+1},a_{l+2}) \geq max(a_{l},a_{l+1},a_{l+2})\cdot min(a_{l},a_{l+1},a_{l+2})$$is established.
Because at least one of $max(a_{l},a_{l+1})=max(a_{l},a_{l+1},a_{l+2})$ and $max(a_{l+1},a_{l+2})=max(a_{l},a_{l+1},a_{l+2})$ is established.
And $min(a_{l},a_{l+1}) \geq min(a_{l},a_{l+1},a_{l+2})$ and $min(a_{l+1},a_{l+}) \geq min(a_{l},a_{l+1},a_{l+2})$ must be established at the same time.
So, only need to enumerate all the intervals of length 2.
Code:
Java

C++

B. Cobb
Solution:
Just enumerate any pair of the last 200 digits.
Consider the pair of last two items, the result is: $n\cdot (n-1)-k\cdot (a_n|a_{n-1})$. Easy to get $a_n|a_{n-1}<n$. Therefore, the minimum value of the result of the pair of the last two items is: $n\cdot (n-1)-100n=n^2-101n$. ($a_n|a_{n-1}<n$ is not rigorous)
Consider the pair of last item and n-100 item, the result is: $n\cdot (n-100)-k\cdot (a_n|a_{n-100})$. Ignore the value of $a_n$, the smallest possible value of $a_n|a_{n-100}$ is 0. Therefore, the maximum value of the result of the pair of the last two items is: $n\cdot (n-100)=n^2-100n$.
We found that the minimum value of $[n,n-1]$ is almost greater than the maximum value of $[n,n-100]$. So enumerating the last 200 digits is very reliable.
Code:
Java

C++

C. Mikasa
Solution:
First, if a number does not appear (assuming the number is x), there must be $x\oplus n> m$. And our task is to find the smallest x.
Let $x\oplus n = y$, we only need to enumerate the first binary bit greater than m bitwise.
For example n=69, m=696:
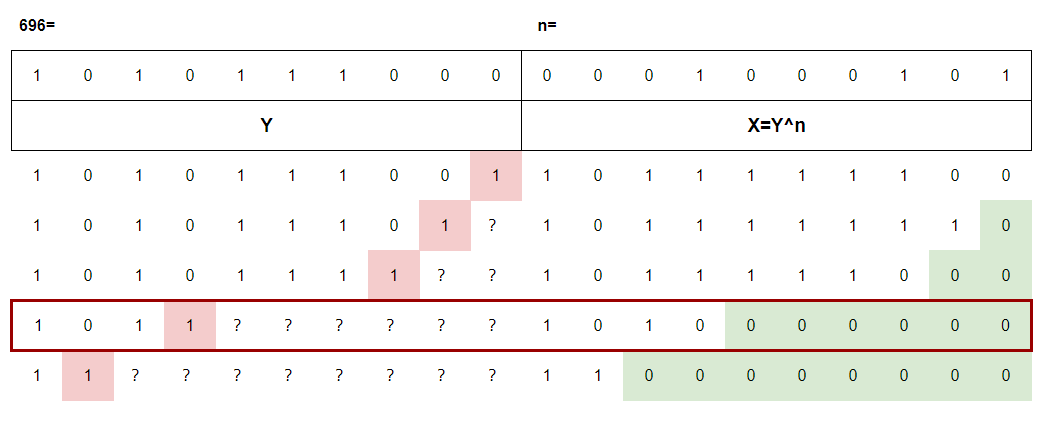
We enumerate the first position where Y is greater than 696 (the red part). The value behind this position can be any value(? part), as long as x is 0 in this position (green part). So we can find out that the result is 640.
The only possible exception is $m=(111...11)_2$. We only need to consider the case of $x=m\oplus (m+1)$ at the end.
Code:
Java

C++

D. Diane
Solution:
Considering the string "aaaaa", and considering all substrings, a appears 5 times, aa appears 4 times, aaa appears 3 times, aaaa appears 2 times, and aaaaa appears once. Therefore, only aa and aaaa do not meet the conditions.
Then Consider the string "aaaa". A appears 4 times, aa appears 3 times, aaa appears 2 times, and aaaa appears once.
So we can think that put these two together, a appears 9 times, aa appears 7 times, aaa appears 5 times, aaaa appears 3 times, and aaaaa appears 1 time.
So our idea is to put x a and x + 1 a to the final string. So we construct a string like aaabaaaa. If n is an odd number, we construct a string like aaabcaaaa.
Code:
Java

C++




