Codeforces Round #722 Kavi on Pairing Duty Solution (Java/C++)

Solution:

Define dp[i] to represent the answer when n=i. We use the case n=4 to explain the solution.

Firstly, consider 2 special cases. As images below:

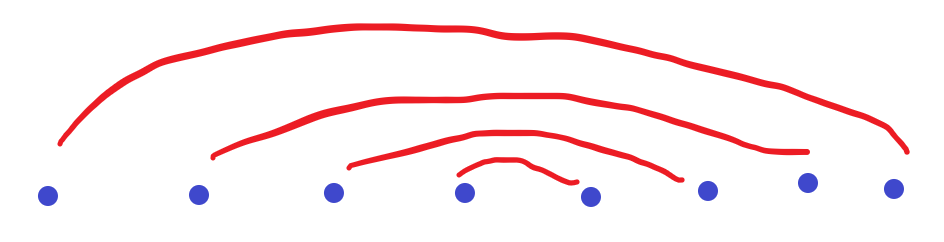
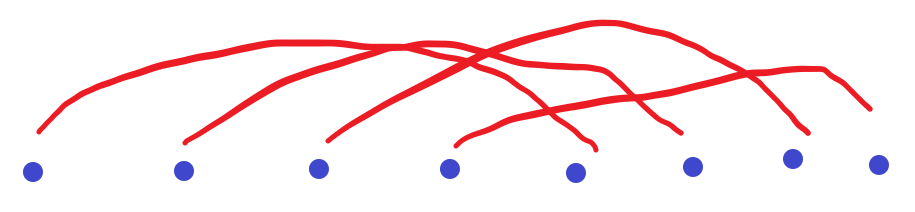
In case warp a segment for all, so we know dp[n]=2+dp[n-1]+?.

Then, in case wrap two segments for all, dp[n]=2+dp[n-1]+dp[n-2]+?.

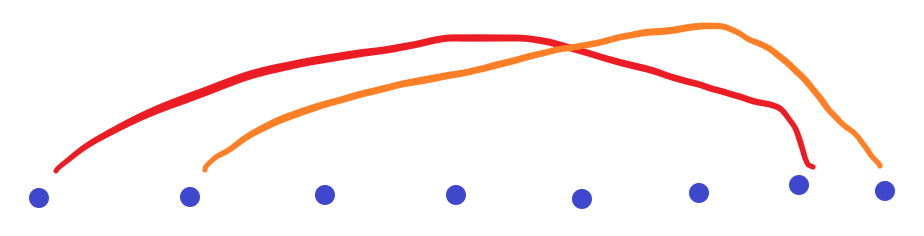
And so on, we know that $dp[n]=2+\sum_{i=1}^{n-1}{dp[i]}+?$.

Now, still one case left: we can split n=4 to two n=2 and make all the length of segment is the same. So, for each factor of n, it is a new answer.

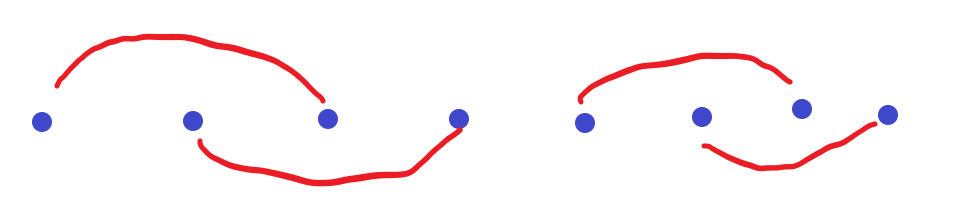
So, $dp[n]=2+\sum_{i=1}^{n-1}{dp[i]}+count\_of\_factor[n]$.

Java

C++